【中学数学】作図　30°・45°　有名角の作図

直角の利用

例題１

$\angle AOB$ が $45°$ になるように線分 $OA$ を作図しなさい。

解答

$45°$ と言えば、直角の半分です。
つまり

1. 直角をつくる
2. 直角を二等分する

この作図方針がすぐ立ちますね。
しっかりと理解・暗記をしておきましょう。

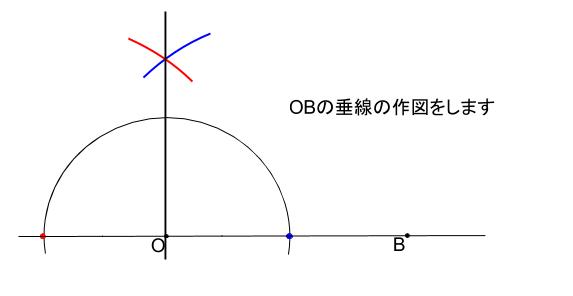
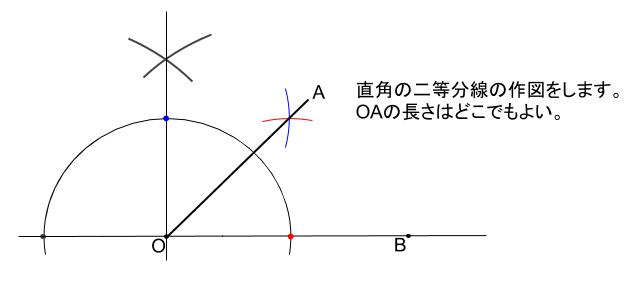
正方形を作図して、対角線を引くと$45°$ の作図ともいえます。
もちろん直角の二等分のさいに作図するひし形が、正方形である必要はありません。

正三角形の利用

例題２

$\angle AOB$ が $30°$ になるように線分 $OA$ を作図しなさい。

解答

$30°$ と言えば・・・
直角の $3$ 等分・・・では作図できません！
角の $3$ 等分は不可能なんです（なぜなのかは激難なので、不可能と覚えておいてね）。

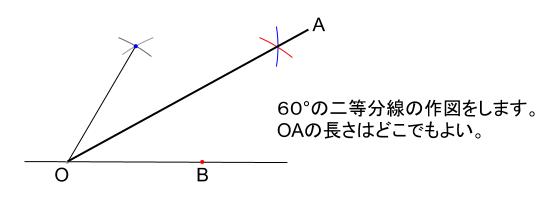
$30°$ といえば、$60°$ の二等分なのです。
では、$60°$ と言えば？

そうです。
正三角形の内角です。
つまり

1. 正三角形の作図で、$60°$ をつくる
2. $60°$ を二等分する

この作図方針です。
しっかりと理解・暗記をしておきましょう。

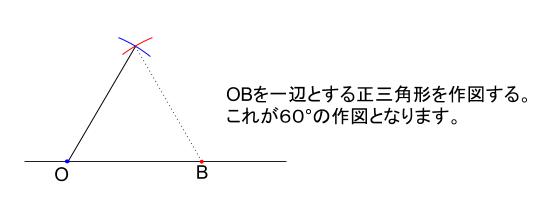
作図が可能な角度とは

その他、$75°$ や$22.5°$ など、作図可能な角度は様々にありますが、これらはいずれも、
$90°$ と $60°$ の角の二等分を利用して作図をします。

$90,45,22.5,11.25・・・$
$60,30,15,7.5・・・$

上であげた角と、それらの和や差で作られる角のみが作図可能な角です。

例えば $75°$ は、
直角から、$60°$ の二等分の二等分である $15°$ を引けば作れますし、
あるいは、$90°$ の二等分と $60°$ の二等分の和で作ることもできます。
$30°$ 度の作図より、その外角の $150°$ を二等分して作ることもできます。

いずれにしろ、$90°,60°$ の角とその二等分された角を利用します。

注　中学数学の範囲をはるかに超えた作図というものはあり、作図可能な角度は上記以外にもあります。
例えば正五角形や正十七角形の作図が可能なので、その内角をつくることができます。

スポンサーリンク